Choosing a Solver¶
odes interfaces with a number of different solvers:
- CVODE
- ODE solver with BDF linear multistep method for stiff problems and Adams-Moulton linear multistep method for nonstiff problems. Supports modern features such as: root (event) finding, error control, and (Krylov-)preconditioning. See
scikits.odes.sundials.cvodefor more details and solver specific arguments. Part of SUNDIALS, it is a replacement for the earliervode/dvode. - IDA
- DAE solver with BDF linear multistep method for stiff problems and Adams-Moulton linear multistep method for nonstiff problems. Supports modern features such as: root (event) finding, error control, and (Krylov-)preconditioning. See
scikits.odes.sundials.idafor more details and solver specific arguments. Part of SUNDIALS. - dopri5
- Part of
scipy.integrate, explicit Runge-Kutta method of order (4)5 with stepsize control. - dop853
- Part of
scipy.integrate, explicit Runge-Kutta method of order 8(5,3) with stepsize control.
odes also includes for comparison reasons the historical solvers:
- lsodi
- Part of odepack, IDA should be
used instead of this. See
scikits.odes.lsodiintfor more details. - ddaspk
- Part of daspk, IDA should be used instead of this. See
scikits.odes.ddaspkintfor more details.
Support for other SUNDIALS solvers (e.g. ARKODE) is currently not implemented, nor is support for non-serial methods (e.g. MPI, OpenMP). Contributions adding support new SUNDIALS solvers or features is welcome.
Performance of the Solvers¶
A comparison of different methods is given in following image. In this BDF, RK23, RK45 and Radau are python implementations; cvode is the CVODE interface included in odes; lsoda, odeint and vode are the scipy integrators (2016), dopri5 and dop853 are the Runge-Kutta methods in scipy. For this problem, cvode performs fastest at a preset tolerance.
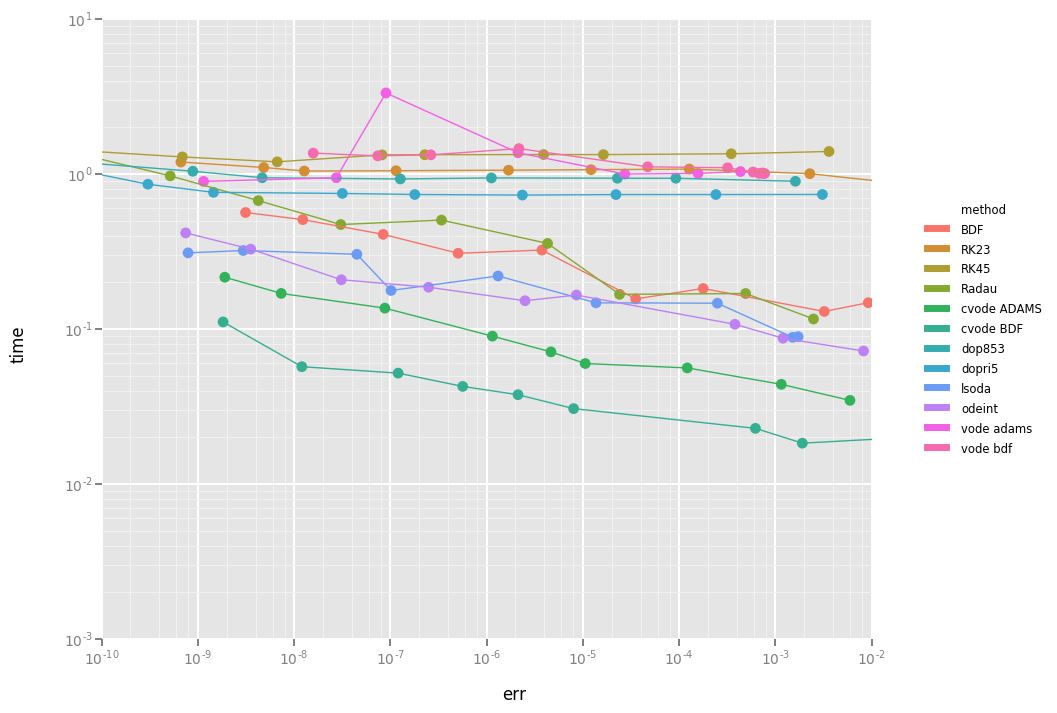
You can generate above graph via the Performance notebook.